外汇交易效用及其计算

    如果说一个人是“理性的”，也就是说，他清楚地知道在两种选择中他偏向于哪一种；再假定他的这种选择倾向是比较稳定的话，那么，他就能够对于这两种选择用数量来表示自己的倾向。对于他所偏向的那种选择，他可加之于较大的数字(即效用)。一旦不同的效用值确定，一个人就可根据效用值的大小作出自己的选择。

下面用三个例子来说明怎样计算效用，即怎样测量偏好。

理解这些例子将有助于读者画出自己的交易曲线。

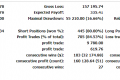
【例1】专做欧元的张先生已经进入了外汇期货市场，定下了自己的目标。一旦这个目标实现，他就可赚到1500美元。他同时也定下了退出该市场的底线，这样，一旦最坏的局面出现，他将输掉900美元。假如对张先生来说，赚到1500美元的效用是10(10是随意定下的)，记作u(1500美元)＝10；输掉900美元的效用是-6(随意指定的)，记作ｕ(-900美元)＝-6。再假定张先生相信成功的概率是1比2。

那么，这项交易的效用就是：

U(交易)＝1/2(10)＋1/2(-6)＝2

注意，交易效用正好处在10和-6之间。

假如张先生对成功概率的判断是2比3，那么，他的交易效用就是：

U(交易)＝2/3(10)＋1/3(-6)＝14/3＝4.7

这个数字正好处在从-6到10之间3比2的地方。

与此类似，如果他判定成功的概率是9比10，那么交易效用就是：

U(交易)＝9/10(10)＋1/10(-6)＝8.4

为了说明“期望效用”(赢和输的效用平均数)和“期望获利”(获利和损失本身的平均数)的不同，我们不妨转到例2。

【例2】假定一项交易如果成功，某人可获利600美元，如果失败，他将损失500美元。再假定成功的概率为0.8。如果获利600美元的效用值人为地定为20，损失500美元的效用值定为10，那么，期望效用就是：U(效用)＝0.8(20)+0.2(10)＝18；而期望获利(用钱来计算)就是：0.8(600美元)+0.2(-500美元)＝380美元

【例3】在上例中，最好和最坏结果的效用分别定为20和10。假如它们分别被定为1和0，那么期望效用就变成：U(交易)＝0.8(1)+0.2(0)＝0.8。注意，当最高效用和最低效用分别定为1和0时，期望效用总是等于最好的结果的概率。选用1和0为最高和最低效用值常常是为了简化计算。

效用概念对有些人来说可能太学究气了，但它实际上可以解释人们在相似的情况下为什么会有不同的选择。两个人在相同的赌局中可能作出不同的决定，但是他们有一点是相同的，即他们都是按照自己认为对自己最有利的路线作出决定的。一个人可能用一笔巨款去冒险，以期得到更多的钱；另一个人则可能不愿用哪怕是一点点的钱去赌博。这并不意味前者胆大或不负责任；也不意味着后者谨慎或过于胆小，他们不过是对赢或输的效用看法不一样。

除了输赢以外，其它效用也会影响一个人的决定。比如时间。有些人偏好用大部分时间去赚更多的钱，另一些人则可能宁愿用这些时间做其它事。有些人喜欢体验由冒险压力而产生的刺激，另一些人则不愿在压力下度过一个个不眠之夜。

总之，不管哪一种效用在影响一个人的决定，最要紧的一点是，每个人要对赢或输的效用有成熟的看法。这种看法将决定一个人是否去冒险，影响到他赢钱和输钱的可能性的高低。